直線上に配置

粉粒体の空気輸送装置
　<粉粒体ハンドリングの部屋(３)>

　ここでは，粉粒体の空気輸送装置の概要を紹介しています。


粉粒体の空気輸送とは：
　輸送元と輸送先をホースや金属配管で接続し，その内部を流れる空気（窒素ガス，酸素ガスなどの場合も有ります）により，粉粒体を輸送する技術です。
　多くは，輸送元にブロータンクやロータリーバルブなどの供給装置が，また輸送先にはタンクやサイロなどの貯蔵装置および，サイクロンやバグフィルタなどの固気分離装置が配置されます。
　なお，空気源としてのブロワは輸送元（圧送の場合）または輸送先に（吸引輸送の場合）置かれ，コンプレッサーの場合は輸送元に置かれます。
　家庭の電気掃除機も，空気輸送装置の１種といえます（以下の「空気輸送装置の分類」で，「吸引輸送方式」に分類されます）。
空気輸送装置の利点：
以下のような利点があり，利用が拡大しています。
（1） 機械的な作動部分が少ない。
　　（コンベア輸送などでは，一般にメンテナンスが大変です。）
（2） 装置を自動化し易い。
　　（使用機器のほとんどが電気や圧力空気で作動します。）
（3） 管路の制約が少ない。
　　（水平配管，鉛直配管以外に斜め配管なども可能です）
（4） 装置の空間が少なくて済む。
　　（機器や配管の容積が比較的少なくて済みます。）
（5） 装置が密閉系となり，粉塵等の飛散を防げる。
　　（装置も装置間も密閉状態となり，気体と粉粒体は分離後放出されます。）
（6） 低速で輸送することにより，管の摩耗や粒体の破砕を防止できる。
　　（プラグ輸送などを採用すれば，これらはかなり改善されます）
　これらをひっくるめると，粉粒体の輸送に関して，(a)自動化，(b)省力化，(c)クリーン化に寄与できるといえます。
　粉粒体のハンドリング作業は，その性状からして，どうしても敬遠されがちですが（一昔前は３Ｋ（きたない，きつい，きけん）と言われたことがあります），供給装置・排出装置･固／気分離装置等も含めた空気輸送装置を有効に活用することにより，快適な環境作りに寄与できます。
空気輸送装置の分類： 　一般的な分類を表にまとめました。
　　　　　　　　　　　
一般的名称 輸送
方式		 輸送
形態		 空気源 輸送方式と
輸送圧		 気流速度
（注１）
(m/s)		 最大
混合比
（注2）
（－）		 　特徴
　（○長所，●短所）
　低濃度
　高速輸送
(dilute-phase 　conveying)		 浮遊
輸送		 分散流 ブロワ 中低圧圧送方式
（0～＋80kPa）
（0～＋0.8
kg/cm2G）		 20～30 一般には
５程度		 ○輸送が安定
●輸送物の破砕
●フロス（注3）
　 の発生
●管の摩耗
吸引輸送方式
（0～－50kPa）
（0～－0.50
kg/cm2G）
　高濃度
　低速輸送
(dense-phase 　conveying)		 プラグ
輸送
（注4）		 プラグ流 コンプレッサ 高圧圧送方式
（0～400kPa）
（0～4.0
kg/cm2G）		 1～6 100
（粒体）
，
200～300
（粉体）		 ○輸送物の破砕が少ない
○フロスの発生がない
○輸送効率が大きい
●圧損失が大きい
(注) 1. 気流速度：管内空気速度のことです。　
2. 混合比：計算式＝輸送物の質量流量（kg/h）／気流の質量流量（kg/h）　
　数値の大きい方が，少ない気体の量で多くの輸送物を運べることになり，効率が良いことを表しています。
3. フロス：プラスチックのペレットなどを空気輸送すると，管内面に薄く融着し，これが時々「カンナ 屑」のように剥がれてきて，各種トラブルの原因になることがあります。
　　この剥がれてきた薄いフイルム状のものを「フロス」といい，長いものでは1ｍ近くになることもあります。
フロス対策としては，(a)気流速度を下げる，(b)気流分離装置（フロスセパレータ）で除去する，あるいは(c)管の内面にローレット（凹凸）加工した「ナーリングパイプ」にすることにより，フロスそのものを発生させないようにします。
  ４.  プラグ輸送は，スラグ輸送ともいいます。  


最近の傾向：
　低濃度高速輸送より，高濃度低速輸送の割合が増えています。
これは，（ａ）輸送効率重視，（ｂ）空気輸送時に，できるだけ破砕（粉化）させたくない，（ｃ）輸送に伴うベンド部の摩耗を防止したい，などが考慮された結果です。


輸送方式と輸送形態の例：
配管内を粉粒体が流れる様子（代表例）を以下に示します。
　　　　　　　
　Ｎｏ 　　　　　　　　　　（１） 　　　　　　　　　（２）
　名称 低濃度高速輸送 　　　　　　高濃度低速輸送
    浮遊輸送（分散流） 　　　　　　プラグ輸送（プラグ流）
　概念図 （輸送方向⇒）
粉粒体が管内で分散，浮遊しながら，速度エネルギーによって輸送されています。輸送物の濃度は管底側で高くなっていますが，堆積層は形成されていません。
　　　　		 （輸送方向⇒）

粉粒体が圧力エネルギーによって，プラグを形成しながらゆっくりと輸送されています。
プラグ通過後には管底に堆積層が形成されますが，次のプラグに取り込まれ，次々に移動していきます。
実際の輸送形態 　（輸送方向⇒）

(SG幅=0.5m×2＝1m)
（気流速度：20m/s）		 　（輸送方向⇒）

（SG全幅=0.5m×2＝1m）
（気流速度：3m/s）
・配管径：内径80mm，・輸送物：ＰＣペレット，・輸送能力：いずれも3ton/h
　　　　　　　　　　　
輸送方式の違い（輸送ラインフローの代表例）：
（1）低濃度高速輸送の装置例
　輸送元に最大吐出圧100kPaGのブロワ(a)を置き，輸送物の供給はロータリーバルブ(b)で行います。

　輸送風量が多く，輸送形態は低濃度高速輸送になります。また，輸送先サイロ(g)の上および末端には，固気分離を目的としたサイクロン(f)，バグフィルタ(h)を置いています。

　連続輸送が可能ですが，ロータリーバルブからのリークが有り，耐圧力が低いために，一般に小能力・近距離輸送用です。

ロータリーバルブを耐圧型にしたものが，“高シール（高圧）ロータリーバルブ”です。

（装置名)　：
　(a)ブロワ
　(b)サイレンサ
　(c)ホッパー
　(d)ロータリーバルブ
　(e)配管
　(f)サイクロン（設置しない場合も有り）
　(g)サイロ
　(h)バグフィルタ


（2）高濃度低速輸送の装置例
　 輸送元に最大吐出圧700kPaGのコンプレッサ①(a)置き，輸送物の切り出しは，輸送元のブロータンク(d)を加圧する圧力と，タンク下部の排出口径を変えて行います。

　　輸送風量が少ないため，輸送形態は高濃度低速輸送になり，輸送先では，サイクロンは一般に不要で，固気分離のためのバグフィルタ(f)も小さくてすみます。

　ブロータンクでは断続のバッチ輸送ですが，を高シール（高圧）ロータリーバルブに置き換えると，若干のリークは許容したうえで，連続的な高濃度輸送が可能になります。

（装置名)　：
　(a)コンプレッサ，
　(b)アキュムレータ，
　(c)流量計，
　(d)ブロータンク
　(e)配管，
　(f)バグフィルタ
　(g)サイロ
　(h)ロータリーバルブ


粉体特性を利用した輸送方式：
　粉体の流動化により著しく圧損が低下する現象を利用した空気輸送装置として，（ａ）エアスライド輸送，（ｂ）垂直気送（垂直輸送），（ｃ）流動化輸送等があります。
　これらについては，粉粒体ハンドリングの部屋(５)で説明しています。

付着性粉体の空気輸送：
　酸化チタンやカーボン等の粉体は付着性が強く，配管内で閉塞しやすい特徴があります。そのため，配管各部で等間隔に，必要に応じて閉塞解除用エアを流したり，配管内に可とう性管（ゴム，ホースなど）を入れるなどの手段が取られます。
　酸化チタン粉体の高濃度空気輸送ラインでの，サイトグラスでの状況を以下に示します。
　　　　　　　　　　　　　　　　　　　　　　　　
＜輸送ラインの例＞


＜管内壁面への粉体の付着と 剥離はくり状況＞
輸送方向

空気輸送装置の規模：
　これまでに実験あるいは設計した実績は，輸送能力で数g/hから数10ton/h 程度，輸送距離で数mから数百mレベル，配管径で数mmから16インチ（400A，400mm）レベルです。

　また，輸送物については，微粉から粗粉，プラスチックペレットのような形状が揃った粉粒体から，最近では古紙（粉砕品），ＲＤＦ（ゴミの粉砕品を棒状に固めたもの），ＰＥＴボトル粉砕品，銅粉と樹脂の混合物など，さまざまな異形物が多くなっています。

　システム的には，低濃度高速輸送方式から高濃度輸送方式に，その中でもブロータンク方式から高シール（高圧）ロータリーバルブ方式へと変わりゆく傾向があります。
     
    高圧ロータリーバルブでの大能力高濃度（プラグ）輸送の状況
   



高圧RV⇒
（配管径6B（インチ） (150A)ラインでのプラグ輸送状況）  
   
 （再生ボタンを押してください）    
   
 輸送能力：約20ton/h (輸送物：PE(ポリエチレン)ペレット)
空気輸送の設計方法の例：
 以下は設計の一手法です。難しい式を使わず簡易的な設計を目指しています。
  (1)浮遊輸送
　　　以下の仮定と手順で計算を進める。
（ⅰ）浮遊輸送時の管内圧力損失ΔPFを，空気の流動による圧力損失ΔPaと粉粒体の流動による追加の
　　　　圧力損失ΔPsの合計と仮定する。
　　　　また，空気の流動による圧力損失ΔPaは，空気だけの流動時（単層流）の圧力損失と等しいと仮定する。
　　　　　　ΔPF＝ΔPa＋ΔPs
　　　　　　ΔPa＝λ･L/D･ρ/2･V 2　 　
　　　　　　　（λ：管摩擦係数，L ：輸送管長さ，D ：管内径，ρ：空気密度，V ：気流速度）　
　　　　　
 
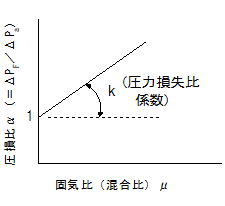
  (ⅱ)圧損比α＝ΔPF /ΔPaとおく。
　　また，これが固気比μに比例すると仮定する。
　　α＝ΔPF/ΔPa＝1＋ΔP s/ΔPa　＝k ･μ
　　　ただし，　μ＝W ／QN　

　（k：粉粒体毎に求まる圧力損失比係数，
　W ：輸送能力，
　QN ：輸送空気の質量流量）　
      
  （ⅲ)起伏のある輸送経路（L）を，水平方向の相当長Leqに換算する。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　Leq＝LH＋Z1×LV＋Z2×N×D　　　　
　　　（LH ：水平管長さ、LV ：鉛直管長さ、N ：ベンド管個数、D ：管内径、Z1･Z2　：係数）

（ⅳ）管内輸送圧力損失ΔPFの算出
　　　ΔPF＝（1＋k･μ）（λ･1/D･ρ/2･V 2 ）×Leq

（ⅵ）輸送全圧力損失ΔPT　の算出
　　　ΔPT　＝（ΔPF＋P ’）×K　　
　　　　　（P ’：空気管圧損・混入圧損・分離機･バルブ･フィルタ圧損等，K：安全率）  
  ＜参考グラフ（PEペレット；浮遊輸送の設計時に利用）＞）
 
 
 (２)プラグ輸送 

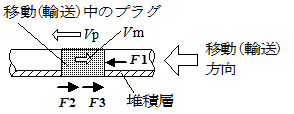
（ⅰ）移動(輸送)中の多数のプラグには，以下
　　　の3力が作用していると考える。

　　　(a)プラグの推進力　　　　　：F1=SΔP
　　　(b)プラグの重力による摩擦力：F2＝fgM
　　　(c)プラグと管壁との剪断力  ：F3＝fkSΔP

  
    
   （S ：断面積，f：管摩擦係数，g：重力加速度，M ：プラグ質量，k：ヤンセンの係数）
   

    これら3力のバランス（F1＝F2＋F3）から，次の関係を得る。
ΔP＝fg/(1-fk)・M／S　		    

   （ⅱ）　ここで，輸送物の実質的な移動速度Vは，V＝Vp－Vmであり，M＝W･L/(Vp－Vm)である。
　　　　（Vp ：プラグの移動速度，　Vm：プラグ内部における，逆方向への粒子移動速度）

　　　一方、Konrad,K.ら の研究を参考にすると，Vp－Vm＝0.542√(gD)＝C√(gD)とおける。

　　　故にM＝W･L/(Vp－Vm)＝W･L/C√(gD)　と置き換えることができる。　
　　　（W：輸送能力，L：プラグ全長，Vp：プラグの移動速度，Vm：プラグ内の粒子の移動速度，C：　定数） 
   
（ⅲ）以上を整理して，次式を得る。
　　　ΔP/L＝K1×W/S√(gD)＋K2　

　　ここで，P：輸送管全長の圧損，L：輸送管の全長，Wa＝W/Sと置き換える。
　　　ΔP/L＝K1×Wa/√(gD)＋K2
　　　（Wa：補正断面積あたり能力，K1，K2：粒体毎の係数）

(Ⅳ)理論の適用
　（a）粉粒体の種類毎に，ΔP/LとWa/√(gD) の関係グラフを作成しておく。
　　　（通常は，気流速度一定（V = 3m/s）でのプラグ輸送を行う）
　　　　　ΔP/L＝K1×Wa/√(gD)＋K2

　（b）輸送経路（L）を水平方向の相当長Leqに換算する。　　
　　　　　Leq＝LH＋Z1×LV＋Z2×NB
　　　　　（LH：水平直管長さ，LV：鉛直管長さ，NB：ベンド管個数，Z1･Z2：係数 ）

（c) 管内輸送圧力損失ΔPF
　　　　　ΔPF＝（K1×Wa／√（gD）＋K2）×Leq　

（d）輸送全圧力損失ΔPT
　　　　　　ΔPT＝（ΔPF＋P’）×K　　
　　　　　　（P’：分離機･バルブ･フィルタ圧損等、K：安全率）

 
   ＜参考グラフ（PEペレット；プラグ輸送の設計時に利用）＞）
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
トップ アイコントップページへ戻る 　　　　　　　　　　　　　　　　　　　　前のページへ　，次のページへ